This problem is a programming version of Problem 143 from projecteuler.net
Let be a triangle with all interior angles being less than degrees. Let be any point inside the triangle and let , , and .
Fermat challenged Torricelli to find the position of such that was minimised.
Torricelli was able to prove that if equilateral triangles , and are constructed on each side of triangle , the circumscribed circles of , , and will intersect at a single point, , inside the triangle. Moreover he proved that , called the Torricelli/Fermat point, minimises . Even more remarkable, it can be shown that when the sum is minimised, and that , and also intersect at .
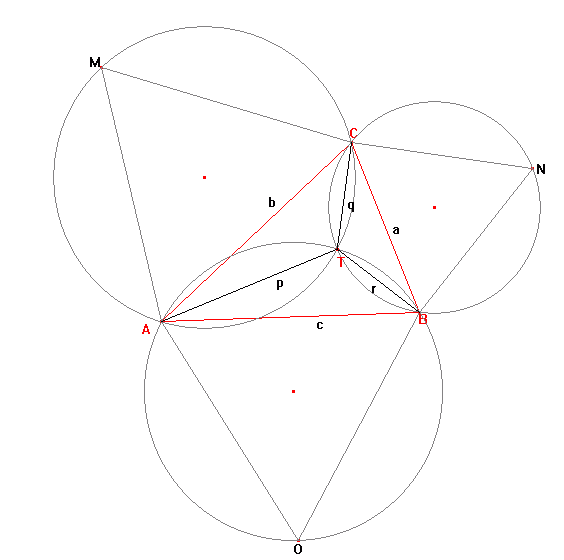
If the sum is minimised and , , , , and are all positive integers we shall call triangle a Torricelli triangle. For example, , , is an example of a Torricelli triangle, with .
Given , print all the side lengths of all Torricelli triangles having . To ensure that no triangle is printed more than once, ensure that . Print the triangles with smaller first, and in case of ties, smaller s, and in case of ties, smaller s.
Input Format
The input contains a single integer, .
Constraints
Input file #1-#2:
Input file #3-#4:
Input file #5-#8:
Output Format
For each test case, output one line for each Torricelli triangle containing three integers separated by single spaces: , and .
Sample Input
1000
Sample Output
399 455 511
Explanation
There is only one such triangle, which is described in the problem statement.