- All Contests
- ProjectEuler+
- Project Euler #177: Integer angled Quadrilaterals.
Project Euler #177: Integer angled Quadrilaterals.
Project Euler #177: Integer angled Quadrilaterals.
This problem is a programming version of Problem 177 from projecteuler.net
Let be a convex quadrilateral, with diagonals and . At each vertex the diagonal makes an angle with each of the two sides, creating eight corner angles.
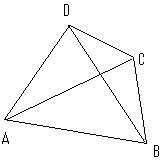
For example, at vertex , the two angles are , .
We call such a quadrilateral for which all eight corner angles have integer values when measured in degrees an integer angled quadrilateral. An example of an integer angled quadrilateral is a square, where all eight corner angles are . Another example is given by , , , , , , , .
Consider to be sorted sequence of quadrilateral angles. What is the number of non-similar integer angled quadrilaterals such that ?
Note: In your calculations you may assume that a calculated angle is integral if it is within a tolerance of of an integer value.
Input Format
The input contains eight numbers .
Constraints
Output Format
Print the only integer which is the answer to the problem.
Sample Input 0
1 1 1 1 1 1 177 177
Sample Output 0
1
Explanation 0
There is exactly one such quadrilateral.