- Prepare
- Algorithms
- Graph Theory
- Even Tree
Even Tree
Even Tree
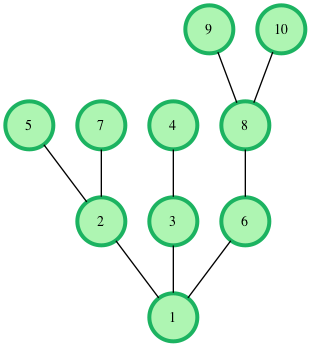
You are given a tree (a simple connected graph with no cycles).
Find the maximum number of edges you can remove from the tree to get a forest such that each connected component of the forest contains an even number of nodes.
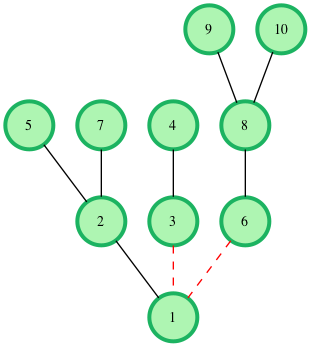
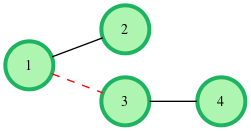
As an example, the following tree with nodes can be cut at most time to create an even forest.
Function Description
Complete the evenForest function in the editor below. It should return an integer as described.
evenForest has the following parameter(s):
- t_nodes: the number of nodes in the tree
- t_edges: the number of undirected edges in the tree
- t_from: start nodes for each edge
- t_to: end nodes for each edge, (Match by index to t_from.)
Input Format
The first line of input contains two integers and , the number of nodes and edges.
The next lines contain two integers and which specify nodes connected by an edge of the tree. The root of the tree is node .
Constraints
Note: The tree in the input will be such that it can always be decomposed into components containing an even number of nodes. is the set of positive even integers.
Output Format
Print the number of removed edges.