Scoring Documentation

1.1. How do I earn badges?

You earn badges by solving challenges on the various practice tracks on our site. If you solve a challenge in an official HackerRank contest, you will earn points towards your progress once the challenge is added to the practice site.

Please note that if you unlock the editorial and solve the challenge in a Skill Track (i.e Non Tutorial track), your score will not be counted toward your progress.

The badges you earn will be added to your profile, and will be visible for other users.

1.2. What are the badges I can earn on HackerRank

You can earn the following badges by solving challenges on HackerRank :

• Problem Solving (Algorithms and Data Structures)
• Language Proficiency
  • C++
  • Java
  • Python
• Specialized Skills
  • SQL

1.3. Medals

Top 25% users in any rated contest will get one of gold, silver and bronze medals. Medal distribution is as follows:

Gold - 4%
Silver - 8%
Bronze - 13%

These medals will be available & visible in your profile.

A rated contest is a HackerRank contest where you have an opportunity to increase (or decrease) your rating based on your performance. The rating is a measure of your proficiency in a particular skill or subject, relative to other users participating. You can identify rated contests by going to our Contests page and selecting the ‘Rated’ filter.

2. Leaderboards

2.1 Domain leaderboard

Each domain on HackerRank (i.e.  Algorithms, Artificial Intelligence, etc) has its own leaderboard.

A user's rating and overall position in the leaderboard is calculated from their performance in the rated contests of that domain. You can find more details in rating section.

For leaderboards in Practice Tracks, a user’s position in the leaderboard is calculated based on the total points they have scored in that domain.

3. Rating

We use an ELO based rating system.

All user start with a rating of 1500. The probability of a user with a rating Ra being placed higher than a person with a rating Rb is equal to:

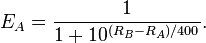
(The image is taken from https://en.wikipedia.org/wiki/Elo_rating_system#Mathematical_details)

With the above formula, we calculate every user’s expected rank in the contest. If your actual rank in the contest is better than your expected rank your rating will increase, otherwise it will decrease. And the amount of change will depend on lot of factors including but not limited to performance of other users, the number of competitions you have participated in. There is also a limit on how much rating you can gain or lose in single event which depends on the number of events you have taken part in.

4. Score Evaluation

4.1 Competitive Games

In a two-player game, there are three components involved:

1. Your Bot
2. Opponent Bot
3. Judge Bot

When you hit "Compile & Test", your bot plays a game against the judge bot. And when you hit "Submit Code", your bot plays against a set of opponent bots.

4.1.1 Game Play

Every submission of yours will play two games with an opponent bot - one with you as the first player and the other with you as the second. Your code should be something similar to this...

                if (player == 1) { //logic}
                else if (player == 2) {//logic}

where player denotes which player you are and is usually given in the input.

4.1.2 State

The goal of your code is to take a particular board state, and print the next move. The code checker takes care of passing the updated state of the board between the bots. The passing continues till one of the bots makes an invalid move, or the game is over.

A bot can't maintain the state of the game within the code. The code is re-run for every move and hence each move should obey the time constraints. The bot can be made to remember a state by writing to a file in its current directory.

4.1.3 Matchup

Your bot plays against every bot ranked 1-10, and then against randomly chosen bots from the rest. It will play against 1 of every 2 bots ranked 11-30, 1 of every 4 bots ranked 31-70, 1 of every 8 bots ranked 71-150, and so on.

4.1.4 Board Convention

Unless specified explicitly in the problem statement, any game played on a board follows the convention as displayed in the format below

The board follows the matrix convention of Mathematics. A board of size m x n has top left indexed (0,0) and bottom right indexed (m-1,n-1). The row index increases from top to bottom, and the column index increases from left to right.

4.1.5 Scoring

Bot v/s Bot games are evaluated based on Bayesian Approximation.  Each game has 3 possible outcomes - win, loss or a draw. A win will have 1 associated with it, 0.5 for a draw and 0 for a loss.

Given μ_i, σ²_i  of Player i, we use the Bradley-Terry full pair update rules.

We obtain Ω_i  and Δ_i  for every player i using the following steps.

For q = 1,......,k, q!=i,

where  q  are the number of bots competing in a game

where β is the uncertainty in the score and is kept constant at 25/6.

where γ_q= σ_i/c_iq  and r(i) is the rank of a player i at the end of a game.

We get

Now, the individual skills are updated using

j = 1,......,n_i

where κ = 0.0001. Its used to always have a positive standard deviation σ.

Score for every player is given as

μ for a new bot is kept at 25 and σ at 25/3.

4.1.6 Midnight re-run

Every midnight (pacific time) we will re-run all the active/valid bots that have been submitted in last 24 hours. They will play against each other according to the above formulas. These extra games will improve the accuracy of the rankings.

4.1.7 Choose your opponent

You can also choose specific bots to match-up against yours. These games will affect your rankings only if a lower ranked bot ends up drawing or winning against a higher ranked bot.

4.1.8 Playoffs

In addition, every midnight there will be another set of games - playoffs. All the bots will be matched based on their rankings and will play a series of games until the top two bots face each other.

4.2 Code Golf

In the Code Golf challenges, the score is based on the length of the code in characters. The shorter the code, the higher the score. The specific scoring details will be given in the challenge statement.

4.3 Algorithmic Challenges

The algorithmic challenges come with test cases which can be increasingly difficult to pass.

The score will be based on the percentage of tests cases which your code passes. For example, if you pass 6 out of 10 tests cases, you will receive the points allotted for those 6 test cases. A correct and optimal solution will pass all the test cases.

4.4 Single Player Games

A single player game involves a bot interacting with an environment. The game ends when a terminating condition is reached. Scoring and terminating conditions are game dependent and the same shall be explained in the problem description.