Absolute Permutation

We define to be a permutation of the first natural numbers in the range . Let denote the value at position in permutation using -based indexing.

is considered to be an absolute permutation if holds true for every .

Given and , print the lexicographically smallest absolute permutation . If no absolute permutation exists, print -1.

Example

Create an array of elements from to , . Using based indexing, create a permutation where every . It can be rearranged to so that all of the absolute differences equal :

pos[i]  i   |pos[i] - i|
  3     1        2
  4     2        2
  1     3        2
  2     4        2

Function Description

Complete the absolutePermutation function in the editor below.

absolutePermutation has the following parameter(s):

int n: the upper bound of natural numbers to consider, inclusive
int k: the absolute difference between each element's value and its index

Returns

int[n]: the lexicographically smallest permutation, or if there is none

Input Format

The first line contains an integer , the number of queries.
Each of the next lines contains space-separated integers, and .

Constraints

Sample Input

STDIN   Function
-----   --------
3       t = 3 (number of queries)
2 1     n = 2, k = 1
3 0     n = 3, k = 0
3 2     n = 3, k = 2

Sample Output

2 1
1 2 3
-1

Explanation

Test Case 0:

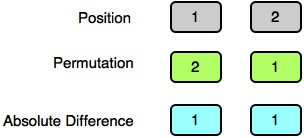
Test Case 1:

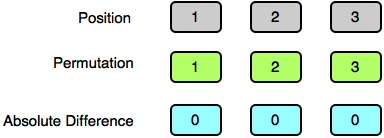
perm(1).png

Test Case 2:
No absolute permutation exists, so we print -1 on a new line.