Fedya is a seasoned traveller and is planning his trip to Treeland. Treeland is a country with an ancient road system which is in the form of a tree structure. cities of Treeland are numbered by positive integers: .
Fedya has not yet decided the starting point (city) of his journey and the cities he will visit. But there are a few things you know about Fedya's trip:
Fedya is fond of travelling to great distances. So if he is currently located in city , his destination will be a city which is most distant from city .
There might be more than 1 such cities. In that case, Fedya will choose a city that was already visited as less times as possible in this journey.
There still might be more than 1 such cities. In that case, Fedya will go to the city with the smallest number.
Fedya has prepared a list of possible journeys. Each one is characterized by two integers - the starting city and the total number of cities to be visited, . For each of them, he is keen to know the total distance travelled by him.
Input Format
The first line of input will contain two space separated integers and - the number of cities and the number of possible journeys.
Then, there will be lines, each of them will contain two space separated integers , denoting the bi-directional road between the cities with numbers and with the unitary length.
Then there will be lines, each of them will have two space separated integers and , denoting a journey.
Constraints
Output Format
For each journey, output the travelled distance on a separate line.
Sample Input
8 7 2 1 3 2 4 2 5 1 6 1 7 1 8 7 4 6 3 4 6 3 7 6 4 6 7 1 2 6
Sample Output
24 16 11 23 24 3 23
Explanation
The tree in question is given in the picture below.
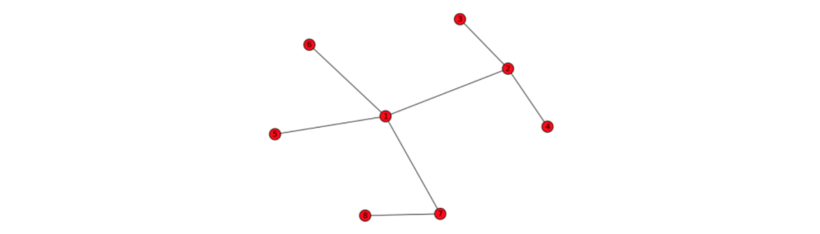
4 6indicates that Fedya starts at 4. Now we see that the most distant city from 4 is 8. Fedya now travels to city 8. From 8, the most distance cities are [4, 3]. As 4 is already visited, he chooses to visit city 3. From city 3, he revisits city 8 and so on. The cities in the order of visit is 4 - > 8 -> 3 -> 8 -> 4 -> 8 -> 3 which sums to 24. Hence, the answer.6 3indicates that Fedya starts at city 6. From 6, the most distant cities are [3,4,8]. In this leg of the journey, no city is visited and hence Fedya chooses to visit the city with the smallest number 3. From 3, he visits 8 and then he ends his trip at city 4 which sums to 3 + 4 + 4 = 11. Hence, the answer.