We use cookies to ensure you have the best browsing experience on our website. Please read our cookie policy for more information about how we use cookies.
  1. Prepare
  2. Algorithms
  3. Game Theory
  4. Nimble Game

Nimble Game

Two people are playing Nimble! The rules of the game are:

  • The game is played on a line of squares, indexed from to . Each square (where ) contains coins. For example:
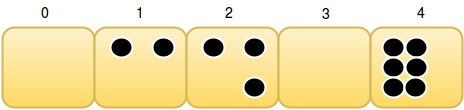
    nimble.png
  • The players move in alternating turns. During each move, the current player must remove exactly coin from square and move it to square if and only if .
  • The game ends when all coins are in square and nobody can make a move. The first player to have no available move loses the game.

Given the value of and the number of coins in each square, determine whether the person who wins the game is the first or second person to move. Assume both players move optimally.

Input Format

The first line contains an integer, , denoting the number of test cases.
Each of the subsequent lines defines a test case. Each test case is described over the following two lines:

  1. An integer, , denoting the number of squares.
  2. space-separated integers, , where each describes the number of coins at square .

Constraints

Output Format

For each test case, print the name of the winner on a new line (i.e., either or ).

Sample Input

2
5
0 2 3 0 6
4
0 0 0 0

Sample Output

First
Second

Explanation

Explanation for testcase:
The first player will shift one coin from to . Hence, the second player is left with the squares . Now whatever be his/her move is, the first player can always nullify the change by shifting a coin to the same square where he/she shifted it. Hence the last move is always played by the first player, so he wins.

Exlanation for testcase:
There are no coins in any of the squares so the first player cannot make any move, hence second player wins.