This problem is a programming version of Problem 90 from projecteuler.net
Each of the six faces on a cube has a different digit ( to ) written on it; the same is done to a second cube. By placing the two cubes side-by-side in different positions we can form a variety of 2-digit numbers.
For example, the square number could be formed:
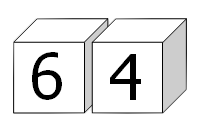
In fact, by carefully choosing the digits on both cubes it is possible to display all of the square numbers below one-hundred: .
For example, one way this can be achieved is by placing on one cube and on the other cube.
However, for this problem we shall allow the or to be turned upside-down so that an arrangement like and allows for all nine square numbers to be displayed; otherwise it would be impossible to obtain .
In determining a distinct arrangement we are interested in the digits on each cube, not the order.
is equivalent to
is distinct from
But because we are allowing and to be reversed, the two distinct sets in the last example both represent the extended set for the purpose of forming 2-digit numbers.
How many distinct arrangements of the cubes allow for all of the first square numbers (..) to be displayed?
Input Format
Each test contains a single line with two numbers - and
Output Format
Output should contain the only number - the answer to the problem.
Sample Input
3 1
Sample Output
55
Explanation
In order to display 3 numbers - 1, 4 and 9 - our only cube should have (1,4,9) or (1,4,6).
That gives us variants for (1,4,9), variants for (1,4,6) and variants for (1,4,6,9) as the intersection to be subtracted.
Now, .