This problem is a programming version of Problem 150 from projecteuler.net
In a triangular array of positive and negative integers, we wish to find a subtriangle such that the sum of the numbers it contains is the smallest possible.
In the example below, it can be easily verified that the marked triangle satisfies this condition having a sum of .
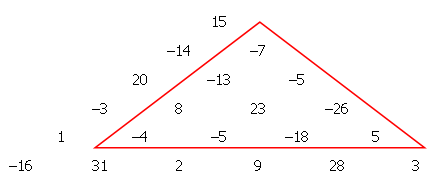
Now, let's extend the problem. Suppose we have such a triangular array with rows, thus there are entries all in all.
Subtriangles can start at any element of the array and extend down as far as we like (taking-in the two elements directly below it from the next row, the three elements directly below from the row after that, and so on).
The "sum of a subtriangle" is defined as the sum of all the elements it contains.
Given , find the smallest possible subtriangle sums. Consider all subtriangles distinct, even though some of them may have the same sums.
Input Format
The first line of input contains two integers and separated by a space.
The next lines contain the entries of the triangle. Specifically, the th following line contains integers, denoting the entries in the th row of the triangle.
Constraints
In files #01-#03:
In files #04-#06:
In files #07-#09:
Output Format
Output lines. The th line contains the th smallest subtriangle sum.
Sample Input
6 5
15
-14 -7
20 -13 -5
-3 8 23 -26
1 -4 -5 -18 5
-16 31 2 9 28 3
Sample Output
-42
-39
-26
-26
-25
Explanation
The input represents the triangle in the image above. As you can see, is the first output since it is the smallest subtriangle sum. Also, note that appears twice because there are two subtriangles with a sum of .