This problem is a programming version of Problem 154 from projecteuler.net
A triangular pyramid is constructed using spherical balls so that each ball rests on exactly three balls of the next lower level.
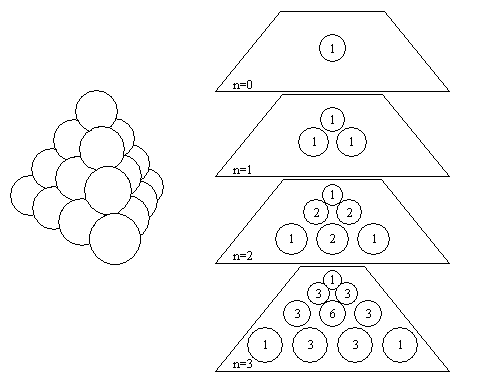
Then, we calculate the number of paths leading from the apex to each position:
A path starts at the apex and progresses downwards to any of the three spheres directly below the current position.
Consequently, the number of paths to reach a certain position is the sum of the numbers immediately above it (depending on the position, there are up to three numbers above it).
The result is Pascal's pyramid and the numbers at each level are the coefficients of the trinomial expansion .
How many coefficients in the expansion of are multiples of ?
Input Format
Each test file contains three lines. First line contains a single number . The second line contains two integers separated by space: and . The third line contains and in the same format.
Constraints
- , are different primes
- answer
Output Format
Output a single integer which is the answer to the problem.
Sample Input
3
2 1
3 1
Sample Output
1
Explanation
As we can see on the picture, there is only one number on the rd layer which is a multiple of - itself.