This problem is a programming version of Problem 161 from projecteuler.net
A triomino is a shape consisting of three squares joined via the edges. There are two basic forms:
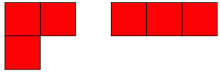
If all possible orientations are taken into account there are six:
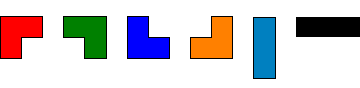
Any by grid for which is divisible by can be tiled with triominoes.
If we consider tilings that can be obtained by reflection or rotation from another tiling as different there are ways a by grid can be tiled with triominoes:
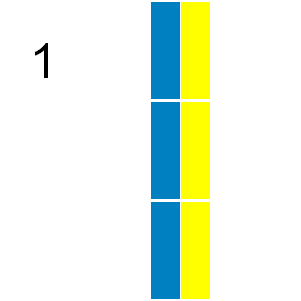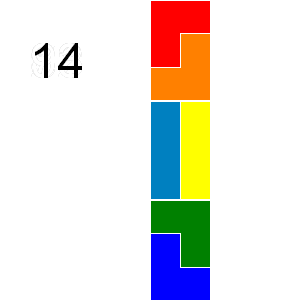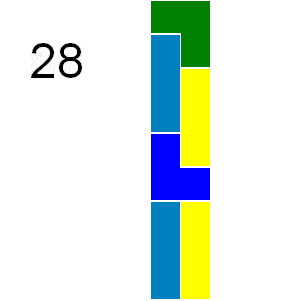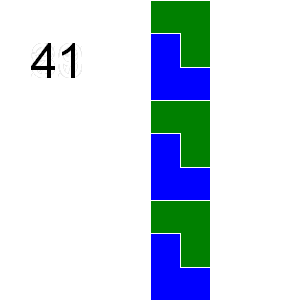
In how many ways can a by grid be tiled in this way by triominoes?
Print answer modulo .
Input Format
First line contains and .
Constraints
is divisible by
Output Format
Print one integer i.e. answer modulo .
Sample Input
2 9
Sample Output
41