This problem is a programming version of Problem 163 from projecteuler.net
Consider an equilateral triangle in which straight lines are drawn from each vertex to the middle of the opposite side, such as in the size 1 triangle in the sketch below.
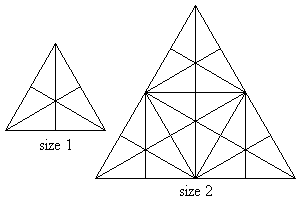
Sixteen triangles of either different shape or size or orientation or location can now be observed in that triangle. Using size 1 triangles as building blocks, larger triangles can be formed, such as the size 2 triangle in the above sketch. One-hundred and four triangles of either different shape or size or orientation or location can now be observed in that size 2 triangle.
It can be observed that the size 2 triangle contains size 1 triangle building blocks. A size 3 triangle would contain size 1 triangle building blocks and a size n triangle would thus contain size 1 triangle building blocks.
If we denote as the number of triangles present in a triangle of size , then
You are given . Find .
Input Format
One integer is given on first line representing .
Constraints
- .
Output Format
Print one integer which is the answer.
Sample Input
2
Sample Output
104