This problem is a programming version of Problem 174 from projecteuler.net
We shall define a square lamina to be a square outline with a square "hole" so that the shape possesses vertical and horizontal symmetry.
Given eight tiles it is possible to form a lamina in only one way: square with a hole in the middle. However, using thirty-two tiles it is possible to form two distinct laminae.
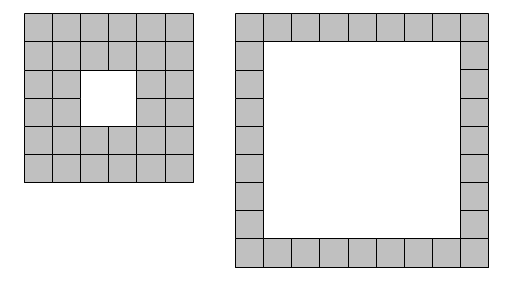
If represents the number of tiles used, we shall say that is type and is type .
Let be the number of such that
is type ; for example, .
Given , calculate .
Input Format
The first line of input contains an integer which is the number of testcases.
Each of the following lines contain one integer .
Constraints
Output Format
For each testcase output the only integer which is the answer to the problem.
Sample Input 0
1
100
Sample Output 0
24
Explanation 0
For :