This problem is a programming version of Problem 246 from projecteuler.net
A definition for an ellipse is:
Given a circle with centre and radius and a point such that , the locus of the points that are equidistant from and form an ellipse.
The construction of the points of the ellipse is shown below.
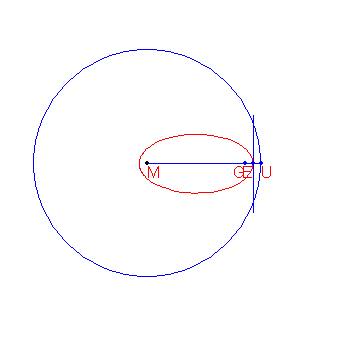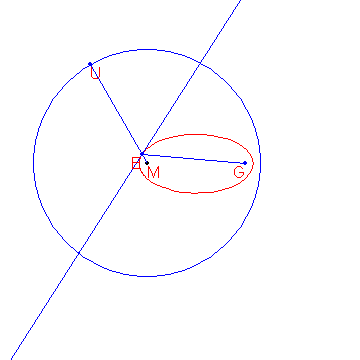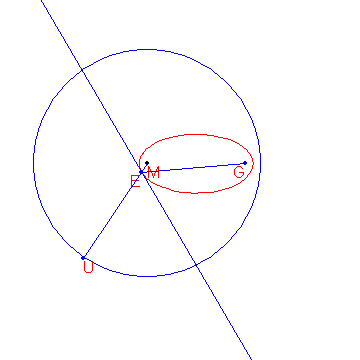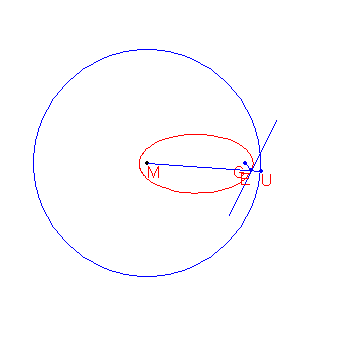
Given are the points and .
Given is also the circle with centre and radius .
The locus of the points that are equidistant from and form an ellipse .
From a point outside the two tangents and to the ellipse are drawn.
Let the points where and touch the ellipse be and .
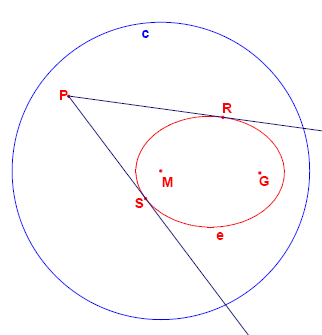
For how many lattice points is angle greater than degrees?
Input Format
First line of each test file contains three integers separated by single spaces: , and .
Second line of each test file contains a single integer .
Third line of each test file contains two integers and separated by a single space which represent the angle in such a way that .
Constraints
- is even
- is acute
Output Format
Print exactly one number which is the answer to the problem.
Sample Input 0
64817 64819 11420
3
30 1
Sample Output 0
4
Explanation 0
These points are , , and .
Sample Input 1
-13896 -13894 43360
3
1 1
Sample Output 1
32