Watson gave Sherlock a collection of arrays . Here each is an array of variable length. It is guaranteed that if you merge the arrays into one single array, you'll get an array, , of distinct integers in the range .
Watson asks Sherlock to merge into a sorted array. Sherlock is new to coding, but he accepts the challenge and writes the following algorithm:
(an empty array).
number of arrays in the collection .
While there is at least one non-empty array in :
- (an empty array) and .
While :
- If is not empty:
- Remove the first element of and push it to .
- .
- If is not empty:
While is not empty:
- Remove the minimum element of and push it to .
Return as the output.
Let's see an example. Let V be .
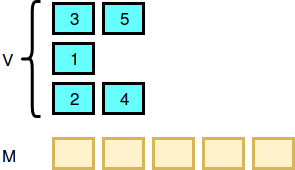
The image below demonstrates how Sherlock will do the merging according to the algorithm:
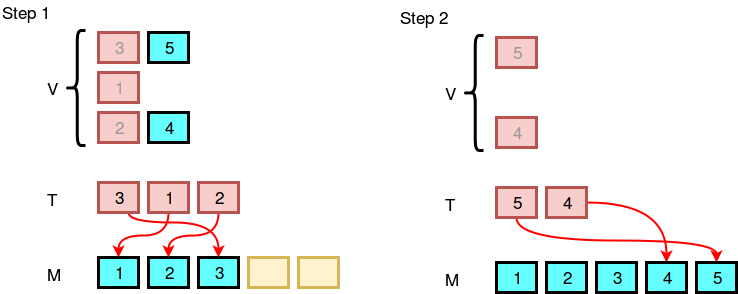
Sherlock isn't sure if his algorithm is correct or not. He ran Watson's input, , through his pseudocode algorithm to produce an output, , that contains an array of integers. However, Watson forgot the contents of and only has Sherlock's with him! Can you help Watson reverse-engineer to get the original contents of ?
Given , find the number of different ways to create collection such that it produces when given to Sherlock's algorithm as input. As this number can be quite large, print it modulo .
Notes:
Two collections of arrays are different if one of the following is true:
- Their sizes are different.
- Their sizes are the same but at least one array is present in one collection but not in the other.
Two arrays, and , are different if one of the following is true:
- Their sizes are different.
- Their sizes are the same, but there exists an index such that .
Input Format
The first line contains an integer, , denoting the size of array .
The second line contains space-separated integers describing the respective values of .
Constraints
Output Format
Print the number of different ways to create collection , modulo .
Sample Input 0
3
1 2 3
Sample Output 0
4
Explanation 0
There are four distinct possible collections:
- .
Thus, we print the result of as our answer.
Sample Input 1
2
2 1
Sample Output 1
1
Explanation 1
The only distinct possible collection is , so we print the result of as our answer.