The Ruler of HackerLand believes that every citizen of the country should have access to a library. Unfortunately, HackerLand was hit by a tornado that destroyed all of its libraries and obstructed its roads! As you are the greatest programmer of HackerLand, the ruler wants your help to repair the roads and build some new libraries efficiently.
HackerLand has cities numbered from to . The cities are connected by bidirectional roads. A citizen has access to a library if:
- Their city contains a library.
- They can travel by road from their city to a city containing a library.
The following figure is a sample map of HackerLand where the dotted lines denote obstructed roads:
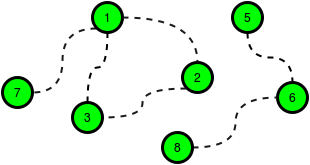
The cost of repairing any road is dollars, and the cost to build a library in any city is dollars. If in the above example and , we would build roads at a cost of and libraries for a cost of . We don't need to rebuild one of the roads in the cycle .
You are given queries, where each query consists of a map of HackerLand and value of and . For each query, find the minimum cost of making libraries accessible to all the citizens and print it on a new line.
Function Description
Complete the function roadsAndLibraries in the editor below. It must return the minimal cost of providing libraries to all, as an integer.
roadsAndLibraries has the following parameters:
- n: integer, the number of cities
- c_lib: integer, the cost to build a library
- c_road: integer, the cost to repair a road
- cities: 2D array of integers where each contains two integers that represent cities connected by an obstructed road .
Input Format
The first line contains a single integer , that denotes the number of queries.
The subsequent lines describe each query in the following format:
- The first line contains four space-separated integers that describe the respective values of , , and , the number of cities, number of roads, cost of a library and cost of a road.
- Each of the next lines contains two space-separated integers, and , that describe a bidirectional road that connects cities and .
Constraints
- Each road connects two distinct cities.
Output Format
For each query, print an integer that denotes the minimum cost to make libraries accessible to all the citizens on a new line.
Sample Input
2
3 3 2 1
1 2
3 1
2 3
6 6 2 5
1 3
3 4
2 4
1 2
2 3
5 6
Sample Output
4
12
Explanation
Perform the following queries:
HackerLand contains cities connected by bidirectional roads. The price of building a library is and the price for repairing a road is .
The cheapest way to make libraries accessible to all is to:
- Build a library in city at a cost of .
- Repair the road between cities and at a cost of .
- Repair the road between cities and at a cost of .
This gives a total cost of . Note that the road between cities and does not need to be repaired each is connected to city .
In this scenario it is optimal to build a library in each city because the cost of building a library () is less than the cost of repairing a road ().
There are cities, so the total cost is .