This problem is a programming version of Problem 128 from projecteuler.net
A hexagonal tile with number 1 is surrounded by a ring of six hexagonal tiles, starting at "12 o'clock" and numbering the tiles 2 to 7 in an anti-clockwise direction.
New rings are added in the same fashion, with the next rings being numbered 8 to 19, 20 to 37, 38 to 61, and so on. The diagram below shows the first three rings.
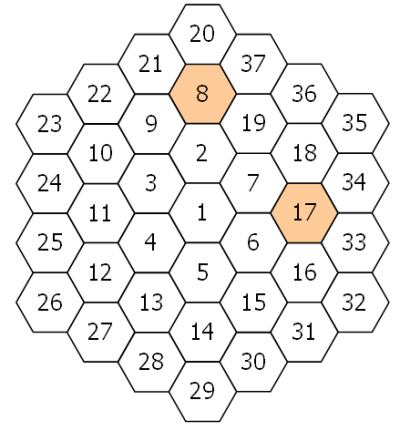
By finding the difference between tile and each its six neighbours we shall define to be the number of those differences which are prime.
For example, working clockwise around tile 8 the differences are 12, 29, 11, 6, 1, and 13. So .
In the same way, the differences around tile 17 are 1, 17, 16, 1, 11, and 10, hence .
It can be shown that the maximum value of is .
If all of the tiles for which are listed in ascending order to form a sequence, the th tile would be .
Find the th tile in this sequence.
Input Format
The first line of input contains , the number of test cases.
Each test case consists of a single line containing a single integer, .
Constraints
Excluding the sample input, there are test files.
For , the th test file satisfies:
Output Format
For each test case, output a single line containing a single integer, the requested tile.
Sample Input
1
10
Sample Output
271
Explanation
As mentioned in the problem statement, the th tile is .