This problem is a programming version of Problem 173 from projecteuler.net
We shall define a square lamina to be a square outline with a square "hole" so that the shape possesses vertical and horizontal symmetry. For example, using exactly thirty-two square tiles we can form two different square laminae:
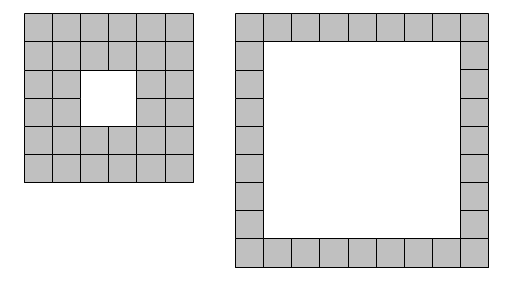
With one-hundred tiles, and not necessarily using all of the tiles at one time, it is possible to form forty-one different square laminae.
Using up to tiles how many different square laminae can be formed?
Input Format
The only integer is given on the first line.
Constraints
Output Format
Print the only integer which is the number of such square laminae.
Sample Input 0
100
Sample Output 0
41
Explanation 0
As written in the statement, for tiles there are ony different laminaes.