This problem is a programming version of Problem 184 from projecteuler.net
Consider the set of points with integer co-ordinates in the interior of the circle with radius , centered at the origin, i.e. .
For a radius of , contains the nine points , , , , , , , and . There are eight triangles having all three vertices in which contain the origin in the interior. Two of them are shown below, the others are obtained from these by rotation.
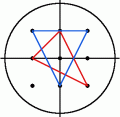
For a radius of , there are triangles containing the origin in the interior and having all vertices in and for the number is .
How many triangles are there containing the origin in the interior and having all three vertices in ?
Input Format
The only line of every test file contains a single integer - .
Constraints
Output Format
Output a single integer - an answer to the problem modulo
Sample Input 0
2
Sample Output 0
8
Sample Input 1
3
Sample Output 1
360
Sample Input 2
5
Sample Output 2
10600