This problem is a programming version of Problem 247 from projecteuler.net
Consider the region constrained by and .
Let be the largest square that can fit under the curve.
Let be the largest square that fits in the remaining area, and so on.
Let the of be the pair (left, below) indicating the number of squares to the left of and the number of squares below .
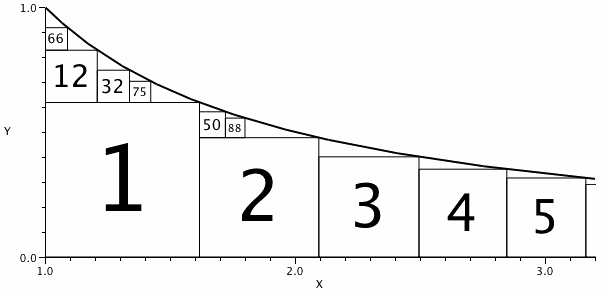
The diagram shows some such squares labelled by number.
has one square to its left and none below, so the index of is .
It can be seen that the index of is (1,1) as is the index of .
is the largest for which the index of is .
What is the -th largest for which the index of is ?
Input Format
First line of each test file contains three integers separated by single spaces: , and .
Constraints
- number of such that index of is
- For every and from the test files the maximum possible answer is less than
Output Format
Print exactly one number which is the answer to the problem.
Sample Input 0
1 0 0
Sample Output 0
1
Sample Input 1
1 1 1
Sample Output 1
50